今日はアインシュタイン記念日。
1905年に、アインシュタインが相対性理論に関する最初の論文「運動物体の電気力学について」をドイツの物理雑誌『アナーレン・デル・フィジーク』に提出した日です。ちなみに当時のアインシュタインはスイス連邦特許局の無名の技師(公務員)でした。
…ということで、今日は相対性理論について、できるだけ簡単に解説してみたいと思います(あまり自信はありませんが…)。
まず、相対性理論には「特殊相対性理論」と「一般相対性理論」の2種類があります。「一般~」は「特殊~」の10年後に発表されたもので、「特殊~」をバージョンアップさせたものです。今日は欲張らずに「特殊相対性理論」に絞って説明をしたいと思います。
そもそも、相対性理論とは
「時間と空間が相対的であるものを明らかにした理論」
です。
そして、特殊相対性理論が到達した結論は次の4つにまとめることができます。
(1)同時性の不一致
(2)時間の流れが遅くなる
(3)空間が縮む
(4)質量が増大する
こう見ると、信じられないようなことばかりですね。でも、これらは全て正しいことなのです!まずは「相対性理論の誕生前夜」から…
相対性理論誕生前夜
例えば、時速60kmで走る電車に並走して、同じく時速60kmで走る車があるとします。この時、車から見ると電車は「止まって」見えますね?では、同じように光の速度(秒速30万km)で動く人から見たら、光は「止まって」見えるのでしょうか?
アインシュタインは16歳の時に「もし自分が光の速さで飛んだら、顔は鏡に映るのだろうか?」という疑問を持ったそうです。顔が鏡に映るには、顔から出た光が鏡に達し、反射して自分の眼に戻ってくる必要があります。しかし、自分が光と同じ速さで動いていたらどうでしょう?光は前に進めず、鏡に届かないのではないでしょうか?しかしアインシュタインは「止まった光」など「ありえない」と考えて悩んだそうです…。←このあたり「天才」の薫りがぷんぷんしますね(笑)
マイケルソン・モーリーの実験
特殊相対性理論が発表される約20年前にアルバート・マイケルソンとエドワード・モーリーという二人のアメリカの科学者によって、地球の東西方向と南北方向で光の速度がどれだけ違うかを測定する実験が行われました。
地球は秒速約30kmで太陽の回りを運動しています。ということは、地球の運動と同じ向きの東西方向に進む光は、地球の運動の向きに対して垂直である南北方向に進む光に比べて、地球の運動の分だけ速度が違って見えるはずです。
マイケルソンとモーリーの二人も、当然、東西と南北とで光の速度は異なるはずだと信じて測定を行いました。しかし、驚いたことに光の速度は2つの方向ともまったく同じ値で観測されました。そうです、光の速度は地球の運動にまったく影響を受けないということが分かったのです。
光速度不変の原理
そこでアインシュタインは、「観測する場所がどんな速さで動いても、光は常に一定の速さで進む」と考えました。つまり「光は誰に対しても秒速30万kmで進む」というのです。もちろんこれは当時の「常識」を覆すものでした。
絶対座標?
当時の(今も?)常識では、宇宙のどこかに「絶対座標」という完全に「静止」している座標系があって、絶対座標に対して止まっている人にだけ、光は秒速30万kmで見え、絶対座標に対して動いている人からは、光速は秒速30万kmより早くなったり遅くなったりして見える、と考えられていました。
絶対座標など存在しない
しかし、この絶対座標はどこにあるのでしょうか?
地球は太陽のまわりを回っているわけですが、太陽は銀河系の中の約2000億個の恒星(みずから輝く星)の1つに過ぎません。そして銀河系は回転をしており、太陽は銀河系を約2億年かけて一周します。また銀河系自身もお隣のアンドロメダ銀河などと引き合って運動しています。こうしてみると「静止している」と言い切れる場所は見つかりそうもありません。
そこでアインシュタインは「絶対座標」という考え方を否定します。そもそも宇宙の中に「静止」している場所を見つけることはできない(というか無意味)と考えたのです。
なぜ光速は誰から見ても「不変」なのか?
「絶対座標」が存在しないことは分かっても、観測者がどのような速度で動いていたとしても、光速は常に30万kmだというのは、にわかには信じがたいですよね?しかし、アインシュタインは若い時の自分の空想やマイケルソンとモーリーの実験に端を発して「有り得べからざることを除去していけば、後に残ったのがいかに信じがたいことであっても、それが事実に相違ない」というシャーロック・ホームズさながらの精神で、光速度不変の原理にたどり着きました。そして実際に、光速度不変の原理は、様々な方法で精度よく実証されています。
では、なぜ光だけが「特別」なのでしょうか?
実は光が特別なわけではありません。光は質量を持ちませんが、質量がゼロであればどんな物質も光速と同じ速度で運動します。つまり光速とは「自然界の最高速度」であり、この最高速度が不変だということなのです。
速度の謎は距離や時間が解き明かす
小学校からお馴染みの式ですが速度は
距離÷時間=速度
という式によって計算されます。もちろん光の速度を計算する場合もこの式を使います。そこでアインシュタインは光速度の不変の謎を解きあかす鍵は、距離や時間の概念にあるんじゃないか、と考えたわけです。まず時間の流れが「一定」だと考えることに対して疑問を持ち、空間の中の2点を結ぶ「距離」についても「一定」とは限らないと考えたわけです。確かにこの2つが「一定」であると考えることは「常識」ではありますが、誰かに手によって証明されたことではありません。
蛇足ですが、ここで私の好きなアインシュタインの言葉を紹介します。
「常識とは偏見のコレクションである」
ガリレイの相対性原理
時代は16世紀にまで遡ります。当時はまだ、地動説よりも天動説が信じられていました。そして、地動説を否定する科学者達は「もし地動説が正しいのならば、球を真上に投げ上げたら、球が空中にある間も地球は動くのだから、球は消して手元に戻ってこないはずだ」等と言って、地動説は間違っていると主張しました。しかしのちにガリレオ・ガリレイは「船が止まっていようと、静かに動いていようと、マスト(船の帆をはる柱)の上から球を落とせば、いつも球はマストの真下に落ちる」という例を上げて地球が動いていたとしても天動説の支持者たちが述べたようなことはおきないと主張しました。
つまり、ガリレオは
「静止している場所だろうが、一定の速さで動いている場所だろうが、そこで起きる物体の運動に違いは表れない」と考えたのです。これを「ガリレイの相対性原理」と言います。
特殊相対性原理
アインシュタインはガリレイの相対性原理の考えをさらに発展させて、「等速直線運動(加速しないでまっすぐに進む運動)している場所では、光の進み方を決める物理法則を含むすべての物理法則が静止した場所と同じように成り立つ」と考えました。これはアインシュタインの特殊相対性原理です。この原理が特殊相対性理論の土台の1つになります。
ふぅ、「前夜」が随分長くなってしましたが、いよいよ本論に入りたいと思います!
疲れた方はここで休憩していただいても構いません
ポイントは「光の速度は誰にとっても一定である」という光速度不変の原理と「等速直線運動している場所では全ての物理法則が"静止"している場所と同じように成り立つ」という特殊相対性原理です。
同時性の不一致
下のイラストを見て下さい。
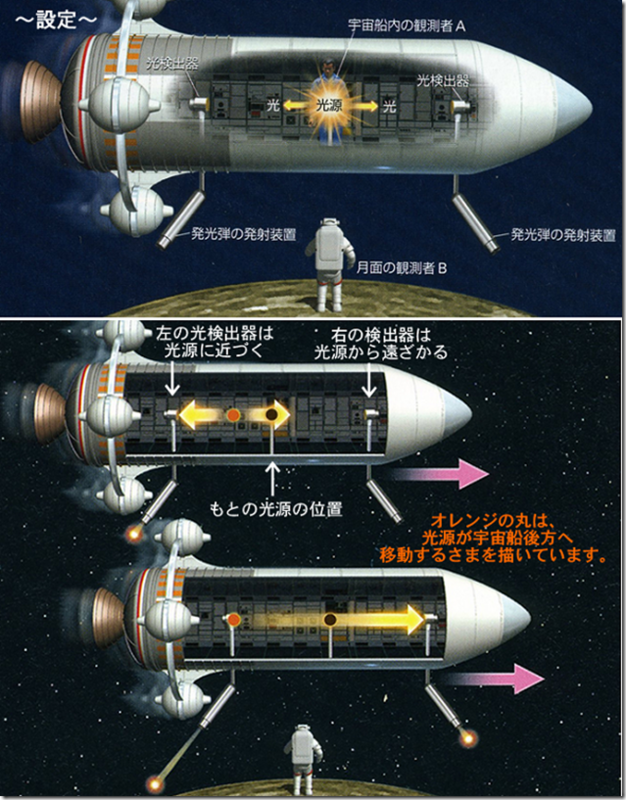
宇宙船が月から見て右方向に光速に近い速度で進んでいるとします。宇宙船の前と後ろには光検出器があり、光が届くと即座に発光弾が発射される仕組みになっています。
まず宇宙船の中央にある光源から同時に光が発せられます。
宇宙船内の観測者Aにとって、光速度不変の原理より、光は左右に同じ速さで進みます。光は光源から等距離にある光検出器に「同時」に到着するので、観測者Aからすると発光弾は同時に発射されることになります。
一方月面の観測者Bから見るとどうでしょうか?Bにとっても光は、光速度不変の原理より、光源の運動に関係なく、左右に同じ速さで進みます。ただし、宇宙船は光が進んでいる間も月から見て右側に進んでいるため、左側の光検出器は光に接近し、光は早く届きます。反対に右側の光検出器は光から遠ざかるので光が遅れて届きます。結果として観測者Bにとっては発光弾は同時に発射されません。
このように光速に近い速度で移動している宇宙船内のAと月面の観測者Bの間で「同時」が一致しないという現象が置きます。
時間の流れが遅くなる
下のイラストを見て下さい。
仮想的に、光速に近い速度で動く宇宙船内に「光時計」を作ったとします。光時計は上部と下部に鏡があり、その間を光が行ったり来たりすることで時間をはかる仕組みになっています。光時計の下部には発光源があります。今は簡単のために光が下部から発せられて上部に届くまでの時間を「1秒」とします。
最初に宇宙船内の観測者Aの立場で考えます。
相対性原理より、宇宙船内は静止しているのと変わらないので、光源から出た光はまっすぐ上に進みます。そして光速度不変の原理より観測者Aにとって光の速度は秒速30万kmです。
次に月面の観測者の立場で考えます。
宇宙船内の光時計の光源から光が出て上部に届くまでの間に、宇宙船は移動しているので、光は斜めに進むように見えます。そして、この月面の観測者から見ても光速度不変の原理より光の速度は秒速30万kmでなければなりません。すなわち「1秒」の間に進む距離(ここでは光時計の長さ)は同じです。しかし、光は明らかに光時計の長さよりも長い距離を移動しています。月面の観測者にとっては、光は「1秒」で進める距離よりも長い距離を進まないと、宇宙船内の光時計の上部に光が届かないように見えるわけです。すなわち月面の観測者にとっては、宇宙船内の光時計で光が上部に達するまでには「1秒」よりも長い時間かかるように見える、というわけです。
仮に、月面の観測者にとって「1.5秒」で光時計の上部に光が達するとしましょう。しかし、あくまで宇宙船内の観測者Aにとっては光が光時計の上部に達するまでの時間は「1秒」です。ということは…?そうです。月面の観測者にとっての「1.5秒」の間に、宇宙船内では「1秒」しか経過していないことになります。
以上より、月面の観測者からすると、宇宙船内の時間は遅れている(ゆっくり流れる)ということになるのです。非常に奇妙な結論ですが、これは「相対性原理」と「光速度不変の原理」から自然と導かれる結論なのです。
「動いている時計は遅れる」の実例
これまで、頭の中で想像した思考実験によって「動いている時計は遅れる(ゆっくり進む)」ということが分かりましたが、このことが実際の実験で確かめられた例はないのでしょうか?
あります!
宇宙からは宇宙線という高エネルギーの放射線が地球に降り注いでいます。そして宇宙線が地球の大気上層部にある原子と衝突すると、ミューオン(ミュー粒子)というミクロの粒子が生まれます。このミューオンは光とほぼ同じ速さで大気中を飛行するのですが、100万分の2秒ほどで壊れて別の粒子に変化してしまうことが分かっています。
光とほぼ同じ速度で飛ぶミューオンが100万分の2秒という寿命の間にどれだけ飛行できるかを計算すると、約600mです。一方地球の大気の厚さは約20kmなので、大気上層部で生まれたミューオンが地表にまでやってくることはないはずです。ところが、地表で大量のミューオンが検出されることが実験で確認されています。どうしてそんなことが起こるのでしょうか?
そうです。これこそまさに「動いている時計が遅れる」実例です。ミューオンの寿命は100万分の2秒だと書きましたが、これはあくまでミューオンが止まっている時の寿命です。実際のミューオンは光速に近い速度で移動しているために、寿命が約50倍に伸びて、厚い大気を通り抜けて地表にまで到達できるのです。
空間が縮む
上のミューオンの実験は面白いことを示唆しています。
もしミューオンと並んで飛行する人がいるとして、その人がミューオンを見たら、ミューオンの寿命は別に長くなってはいないのです。ミューオンと並んで飛行している人からすれば、ミューオンは静止しているので、ミューオンの寿命は100万分の2秒のままです。しかし、大気の上層部で生まれたミューオンが大気層を通り抜けて地表にまで到達している、という事実に変わりはありません。そこで新たな真理が生まれます。それは「動くものは、進行方向の長さが縮む」ということです。
ミューオンと並んで飛んでいる人にとっては、ミューオンは止まっていて、地球の大気層の方が光とほぼ同じ速度で動いていると考えます。すると、動いている大気は進行方向の長さが縮むので、大気の厚さが20kmから数百mになってしまうのです。これにより、100万分の2秒という寿命で600mしか進めないはずのミューオンが地表に到達することができるのです。
これもにわかには信じがたいことですが、動いているものの長さは止まっている時に測った長さよりも短く計測されるという性質を持っているのです。時間と同様に空間的な長さも相対的であることを明らかにしたのが相対性理論なのです。
質量が増大する
相対性理論は光速度不変の原理と相対性原理を土台にして、時間や空間の不思議な性質を明らかにしました。ですが、光の速度には、不変であるということ以外にも特別な意味があることにアインシュタインは気づきました。それは「光速はこの世で実現できる最高の速度だ」ということです。つまり速度には超えられない上限値があるのです。
しかし、そうだとすると大きな疑問が生まれてきます。
電圧をかけるなどして、電子(負の電荷をもつ粒子)に電気的なエネルギーを与えて、加速することを考えましょう。ふつうに考えれば、エネルギーを与え続ければ、電子の速さは際限なく大きくなっていきそうです。しかし、速さに上限があるなら、電子にいくらエネルギーをつぎ込んでも光速には到達できないことになります…どういうことでしょうか?
上のイラストを見て下さい。
止まった電子にエネルギーEを与えて、光速の86.6%まで加速できたとします。特殊相対性理論によると、さらに同じエネルギーEを与えても光速の7.7%分しか加速できません。さて加速に使われなかったエネルギーはどこに消えてしまったのでしょうか?
高校で習う運動方程式によると
です。(m:質量、a:加速度、F:力)
これより
なので、加速度は与える力が大きいほど大きく、質量が大きいほど小さくなります(これは直感的に理解できることだと思います)。
上の例でエネルギーを加えるのは電子に力を与え続けることに相当しますが、エネルギーを与えても(力を加え続けても)たいして加速をしないのは、光速に近くなった電子の質量(m)が増えて、力(F)の効果を打ち消しているからだ、と考えるしかなさそうです。
つまり、特殊相対性理論では
「物体は光速に近づくほど加速しにくくなる、すなわち『質量』が増える」
という結論になるのです。
ちがう言い方をすればこうなります。
「エネルギーは質量に変わった」
そして、この事を表した有名な式が
です。(E:エネルギー、m:質量、c:光速)
従来の科学ではエネルギーと質量は違うものだと考えられていましたが、アインシュタインはエネルギーと質量が同じものであることに気づいたのです。
また、エネルギーが質量に変わるのと同様に、質量がエネルギーに変わることもあります。その代表例が原子力発電で使われるウランの核分裂反応です。ウランの原子核が分裂して複数の原子核になるとき、約0.1%の質量が減ります。その質量は膨大な量の原子力エネルギーとして放出されます。
もし、1円玉5枚の質量(5g)をすべてエネルギーに変えることができるとすると、東京ドーム1杯分(124万キロリットル)の20℃の水を沸騰させることができます。
特殊相対性理論の限界
最後に特殊相対性理論の限界をお話しておきます。
特殊相対性理論では扱えないものが2つあります。それは
・加速度運動
・重力
の2つです。
そして、この2つを扱える理論として特殊相対性理論をバージョンアップした理論が一般相対性理論です…
ふぅ~。
いやあ、長くなりました。
多分このblogの最長記録です。
最後まで読んで下さった方はかなり少数派だと思います。
ありがとうございますm( )m
一般相対性理論については、またいつか機会があったら書いてみたいと思います(^_-)-☆