昨日放送されたNHK Eテレ「テストの花道」に出演させていただきました。前回8月に続いて2回めになります。今回のテーマは「ゴールから考える!」でした。[※ 再放送は10/19(土)午前10時~]
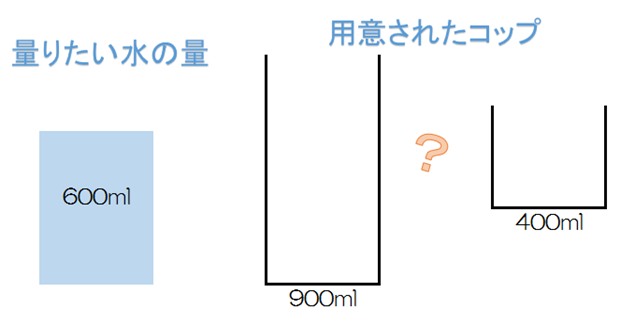
900mlと400mlのコップを使って600mlを量る
「ゴールから考える」のトレーニングとして最初にやった問題はこれです。
どうしたら良いでしょう?なかなか手ごわそうですね…(・・;)
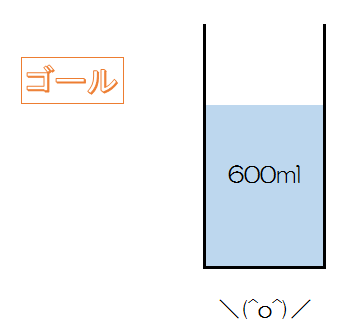
さあ、ゴールをイメージしましょう。600mlの水は400mlのコップには入りませんから、最後に水は900mlのコップに入っているはずですね。つまり、私たちがイメージするべきゴールはこうです。
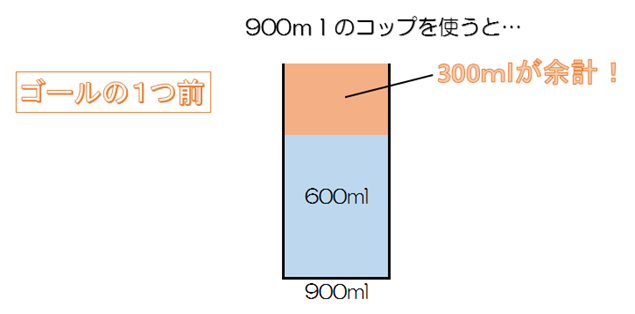
ではこのゴールの1つ前はどのような状態でしょう?それは…
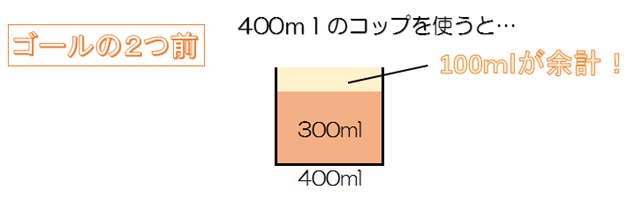
そうなんです!ゴールの1つ前を考えれば300mlを量り取れればいいことが分かります。と、言っても300mlを量るのもそう簡単ではありませんね…そこで!さらにこの1つ前(ゴールの2つ前)を考えてみましょう。今度は400mlのコップを使います。
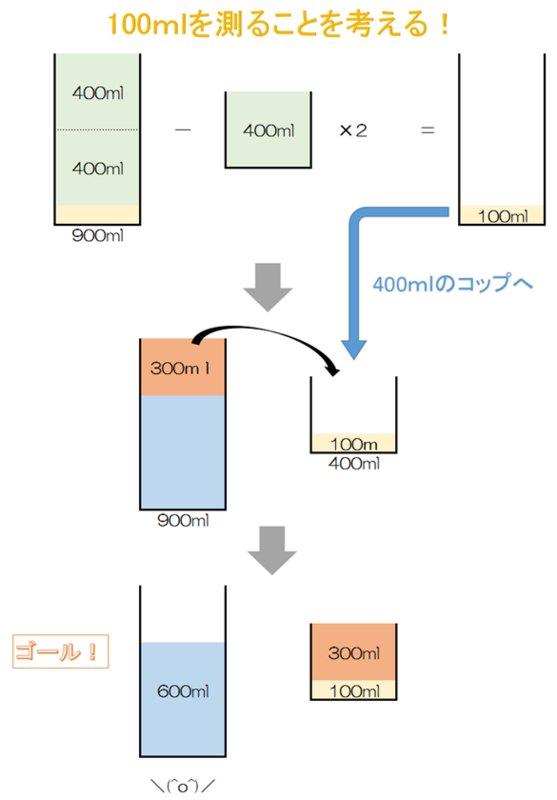
と、100mlが余計なことが分かります。つまりこの問題は100mlを量り取ることさえできれば、上のプロセスを逆にたどることで正解を導くことができるのです!具体的には次のようにします。
ちなみにスタジオでは所さんが見事に正解されていました。さすが!
「ゴールから考える」を証明に活かす!(例:相加・相乗平均)
証明というのは、仮定から結論が導かれるプロセスを論理的に表すことです。
証明を苦手にしている生徒さんはたくさんいます。特に
「どう始めたらいいか分からない…(・・?」
と、最初の糸口が見つからない人が多いようです。そんなときこそ「ゴールから考える」の出番です!証明問題というのは先に結論がみえているので、「ゴールから考える」視点が非常に役立ちます。
数IIで出てくる「相加平均・相乗平均の関係式」の証明を例題にして、「ゴールから考える」の使い方を見て行きましょう。
【例題】
証明に入る前に相加平均と相乗平均の違いを確認しておきますね(^-)-☆
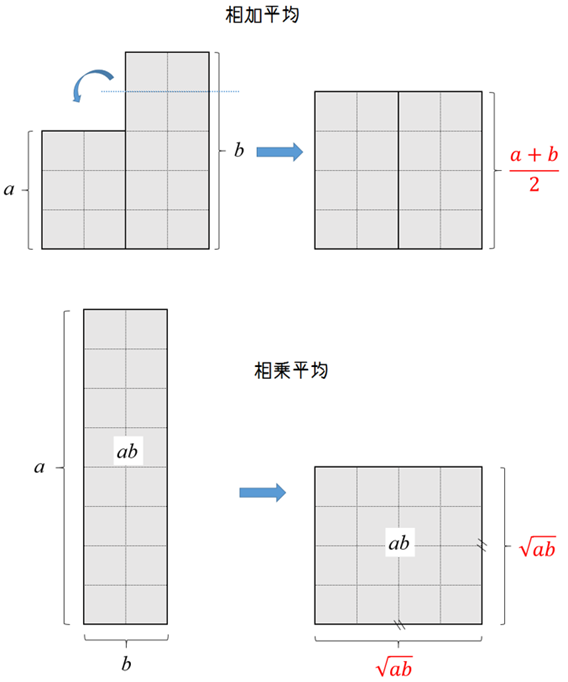
次の図のように相加平均というのはまさに「高さの違うものを平らに均(なら)す」イメージですが、相乗平均はある長方形と同じ面積の正方形を作ったときの一辺の長さのイメージです。
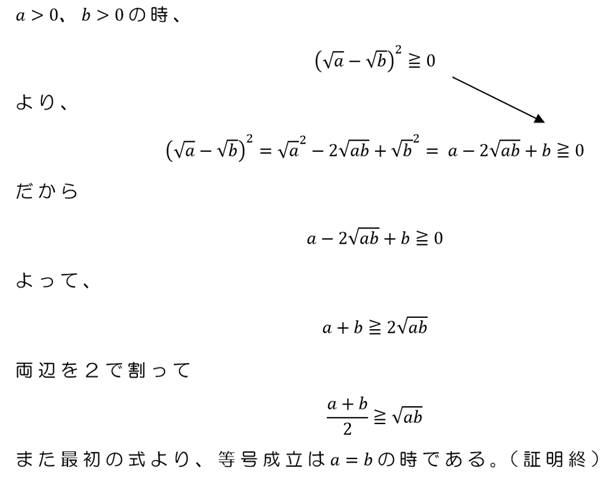
さて、それでは証明の糸口を見つけるためにゴールから考えてみましょう。
次のようになりまsね。
特に条件がないのに0以上になるということは…
と考えられればしめたものです。以上を逆にたどれば、証明の完成です!
【解答例】
逆の視点を持てば、ヒラメキが必然になる!
「ゴールから考える」という逆の視点を持って問題を解決すると、この視点を持たない人は
「なんてヒラメキのある人なんだっ!∑(・ω・ノ)ノ」
と驚いてくれます。でも当人は特別なインスピ―レーションに任せて解いているわけではありません。至極自然の道筋をたどって解いているはずです。つまり「ゴールから考える」という視点を持てるようになれば、他人にとってはヒラメキであることが自分にとっては必然になります。
また、ものごとを色々な角度から見られるようにするというのは数学を学ぶ大きな目標の一つですが、「逆の視点」は、正攻法以外の第2の視点としては最も簡単なものです。柔軟な発想を手に入れたいと思う人はまずこの「ゴールから考える」という逆の視点を磨いてみてください。そうすれば第3の視点、第4の視点もきっと持てるようになります。
「テストの花道」さんにまた声をかけていただいたことはとても励みになりました。数学を苦手な人を1人でも減らしたい、数学を学ぶ意味と意義、それに楽しさをたくさんの人に知ってもらいたいというのは私のライフワークですので、TV出演という機会は大変ありがたいです。これらからも精進します!
昨日の詳しい放送内容はコチラ。番組の後半ではWコロンのねづっちさんが「ゴールから考える」をなぞときに応用されていて面白かったです!