
たとえば、ちょっと本格的に統計を学ぼうとすると、Σ(シグマ)記号を避けて通ることはできません。数式が少なめの入門書を読み終えて、さあ、本腰を入れて勉強しよう!と思った矢先、Σ記号のせいで心折れてしまった人は少なくないはずです。それくらい、Σ記号は、数学が苦手な方からは敬遠されています。でも、慣れるとこれほど便利な記号はありません。この機会に是非攻略してしまいましょう!
記事の最後には「loom」を使った動画解説のリンクもありますので、よろしければぜひご覧ください。
Σの意味
Σ記号の意味を掴むためにまずは具体例から入りましょう。例えば
\begin{align}
\displaystyle \sum_{k=1}^{3} 2k \
\end{align}
は「 の
に 1 から 3 までの数を順々に代入して足したもの」という意味になります。
式でかけば
\begin{align}
\displaystyle \sum_{k=1}^{3} 2k &= 2 \cdot \color{red}{1}+2 \cdot \color{red}{2}+2 \cdot \color{red}{3} \\
&= 2+4+6 \\
&= 12
\end{align}
です。同様に
は「 の
に 2 から 5 までの数を順々に代入して足したもの」という意味で
\begin{align}
\displaystyle \sum_{k=2}^{5} k^2 &= \color{red}{2}^2+ \color{red}{3}^2+ \color{red}{4}^2+ \color{red}{5}^2 \\
&= 4+9+16+25 \\
&= 54
\end{align}
と計算されます。
数列の記号を使ってΣの意味を一般化しておきましょう。

Σは英語で和を表す“Sum”の頭文字Sに相当するギリシャ文字の大文字です。
また、「k」の代わりに別の文字を使っても構いません。「」を表すのに
や
のように書くこともできます*1
さらに初項 からの和でなくても、例えば「
」のような数列の途中から始まる和も
\begin{align}
\color{red}{ \displaystyle \sum_{k=3}^{n} a_k=a_3+a_4+a_5+⋯+a_n}
\end{align}
と表せます。

Σの計算公式

Σの計算公式の数式による証明は本記事の末尾にまとめますが、先に、直観的とは言い難い(ii)自然数*2の和、(iii)平方数*3の和、(iv)立方数*4の和について、図解してみたいと思います。
自然数の和のΣを図解
\begin{align}
\displaystyle \sum_{k=1}^{n} k &= 1+2+3+⋯+n \\
&= \frac{n(n+1)}{2}\
\end{align}
について。
下の図のようにブロックを1個、2個、3個、4個、5個と並べたものを用意します。
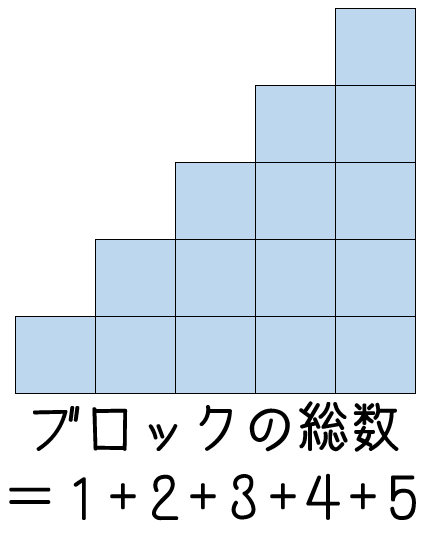
このブロックの総数は 個ですね。
これと同じものをもうひとつ用意して、下の図のように組み合わせると、
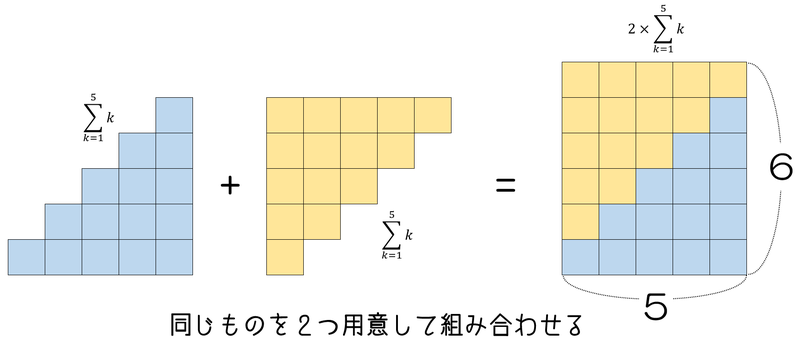
となりますから、
\begin{align}
\displaystyle 2 \times \sum_{k=1}^{5} k=5 \times 6 \Rightarrow \sum_{k=1}^{5} k= \frac{5 \times 6}{2}=15 \
\end{align}
です。
同じように考えて、公式を導きます。
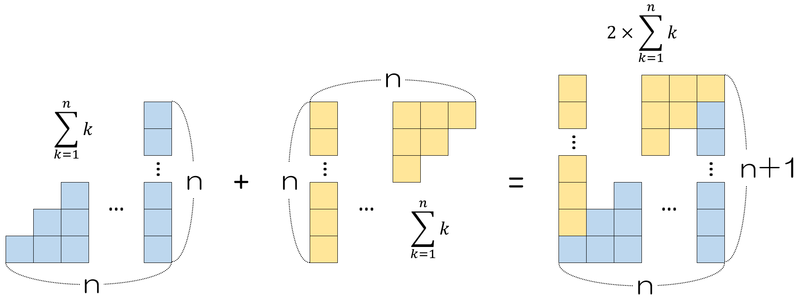

平方数の和のΣを図解
\begin{align}
\displaystyle \sum_{k=1}^{n} k^2 &= 1^2+2^2+3^2+⋯+n^2 \\
&= \frac{n(n+1)(2n+1)}{6}\
\end{align}
について。
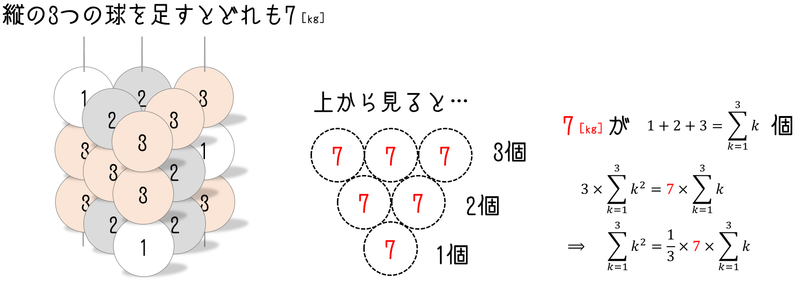
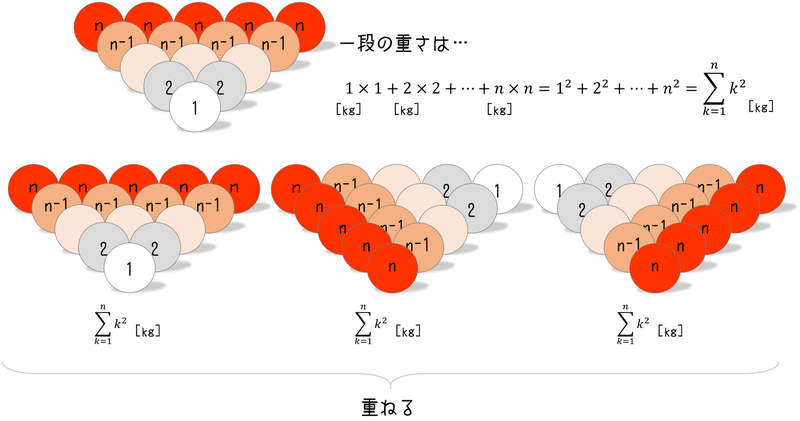
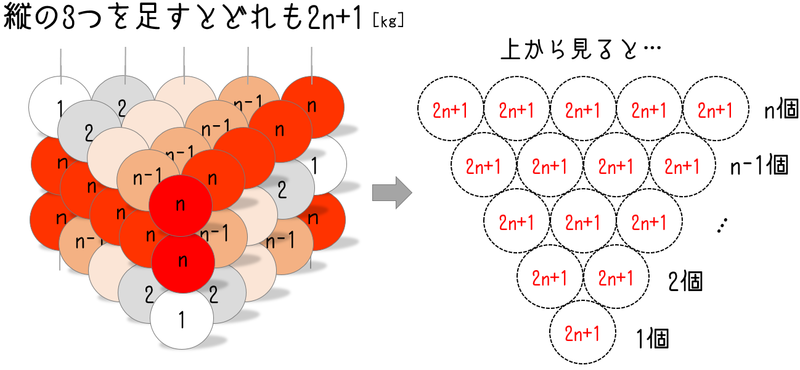
1kgの球を1個、2kgの球を2個、3kgの球を3個、下の図のように三角形状に並べます。次に、同じ6個の球を並べ方を変えて3段に重ねます。
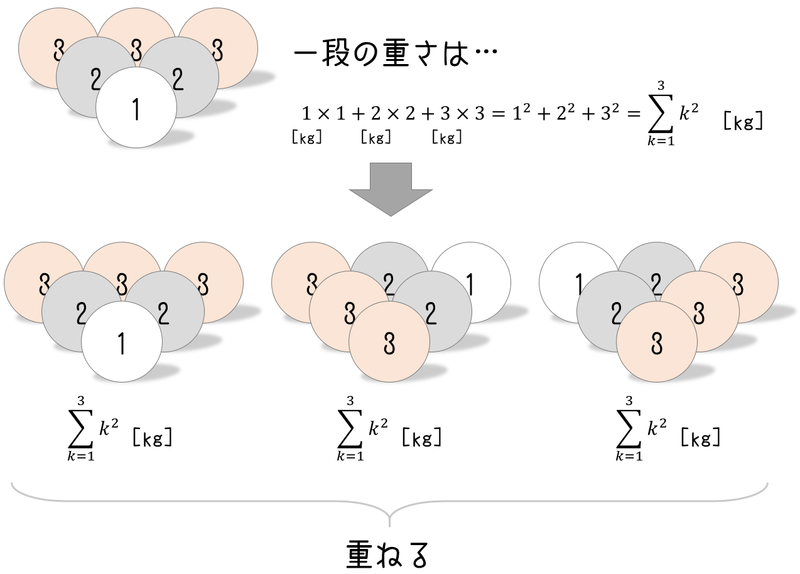
一段の重さは [kg]と表せるので出来上がった三段(計18個)の球の重さの合計は
[kg] です。
同じように考えて、公式を導きます。

立方数の和のΣを図解
\begin{align}
\displaystyle \sum_{k=1}^{n} k^3 &= 1^3+2^3+3^3+⋯+n^3 \\
&= \left\{ \frac{n(n+1)}{2} \right\}^2 \
\end{align}
について。
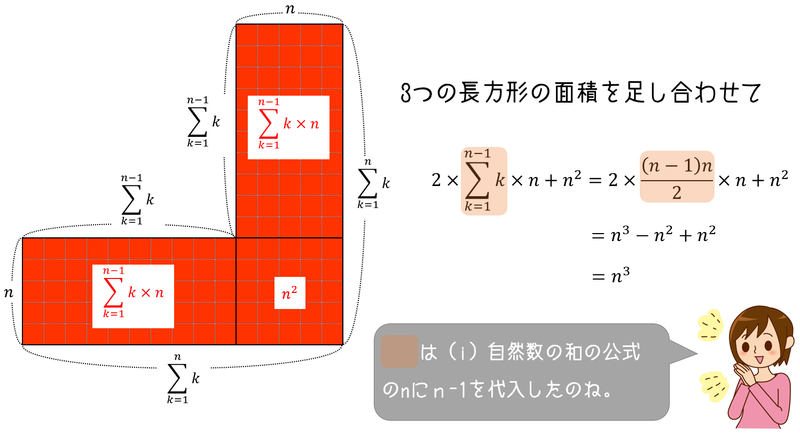
下の図のように、一辺の長さが の正方形の面積を考えます。

実は(上の図のように考えると)、この正方形の面積は と表せます。
つまり、 です。
この考え方を使えば、公式が導けます。


ちなみに、上の図の逆L字部分(赤い部分)の面積が になることは次のように考えれば、確かめられます。
Σの性質(なぜΣ記号は便利なのか?)
Σ記号が便利なのは、これまで と書いていたものを、
と簡明(書き連ねる必要がない)かつ厳密に(…を使わずに)書くことができるという点ももちろんありますが、何より次の分配法則のような性質があるからです。

この性質があるからこそ、定数と自然数と平方数と立方数の和の公式さえ用意しておけば、非常に多くの数列の和を求めることができるのです。
(例)
Σの計算公式の証明
(i)定数の和のΣ
の後ろに
が隠れていると考えます。
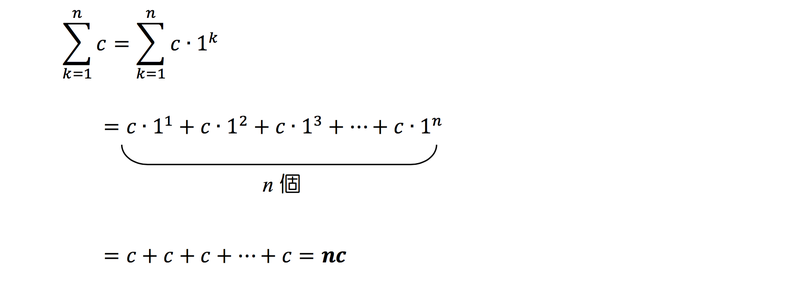
(ii)自然数の和のΣ
\begin{align}
\displaystyle \sum_{k=1}^{n} k=1+2+3+⋯+n=S
\end{align}
としましょう。ここで、次のように考えると
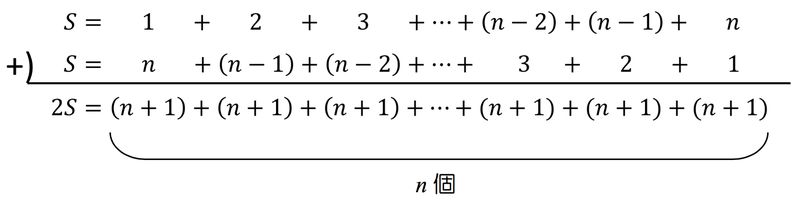
\begin{align}
\ 2S=(n+1) \times n=n(n+1)
\end{align}
となりますね。両辺を2で割れば
\begin{align}
\displaystyle S= \sum_{k=1}^{n} k= \frac{n(n+1)}{2}\
\end{align}
を得ます。
(iii)平方数の和のΣ
ここからは少々厄介です。まず、乗法公式
\begin{align}
\ (a+b)^3=a^3+3a^2b+3ab^2+b^3
\end{align}
を使って(として)
\begin{align}
\ (l+1)^3-l^3=3l^2+3l+1
\end{align}
という恒等式(文字にどんな数字を入れても成り立つ式)を作ります。そして、に1、2、3、…、nを順次代入して、次のように一気に足し合わせます。
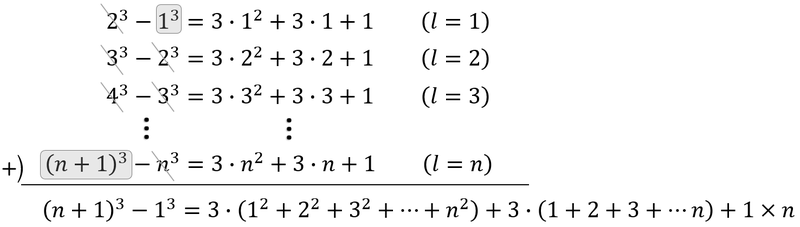

両辺を3で割って
\begin{align}
\displaystyle \sum_{k=1}^{n} k^2= \frac{n(n+1)(2n+1)}{6}\
\end{align}
(iv)立方数の和のΣ
方針は上の(iii)と同じです。ただし、今度は
\begin{align}
\ (a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4
\end{align}
を使います*5これを利用して( を代入して)
\begin{align}
\ (l+1)^4-l^4=4l^3+6l^2+4l+1
\end{align}
という恒等式(文字にどんな数字を入れても成り立つ式)を作ります。そして、(iii)と同じように に1、2、3、…、nを順次代入して、一気に足し合わせます。
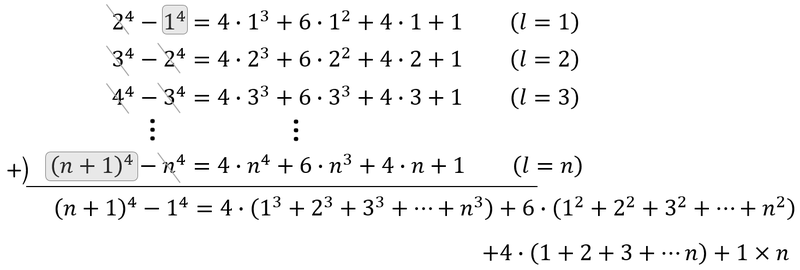

両辺を4で割って
\begin{align}
\displaystyle \sum_{k=1}^{n} k^3= \left\{ \frac{n(n+1)}{2} \right\}^2 \
\end{align}
講演のご依頼をお受けします。お気軽にお問い合わせください。
関連書籍
本記事と関連する内容は、下記の拙書でもご覧いただけます。
動画解説
本記事の内容をクラウド画面録画ツールの「loom」を使って解説しています。ご興味のある方はぜひご覧ください。
今後こそΣ記号を攻略しよう!①(使い方)
今度こそΣ記号を攻略しよう!②(自然数の和の図解等)
今度こそΣ記号を攻略しよう!③(平方数の和の図解)
今度こそΣ記号を攻略しよう!④(立方数の和の図解)

