
「ユークリッドの互除法」は、2 つの自然数(正の整数)の最大公約数を求めるための手法としてよく知られています。
この記事ではまずその手順を紹介し、その後互除法の図形的イメージとこの方法で最大公約数が求まることの証明を書いていきます。最後の証明は少々難しいですが、よろしければ最後までお付き合いください。
最後には、この記事の動画解説リンク(loom)を付けておきましたので、ご興味があれば、そちらもご覧いただければ幸いです。
ユークリッドの互除法の手順
ユークリッドの互除法の手順は次の通りです。
- 大きい方の数を小さい方の数で割る
- 割り切れなければ①の「割った数」を①の「余り」で割る
- 割り切れなければ②の「割った数」を②の「余り」で割る
- ……
これを繰り返し、初めて割り切れたとき「割った数」が最大公約数です。
「互除法」というのは、割り切れるまで互いに(かわるがわる)割り算(除算)を続けることを意味します。以下は、フローチャートです。
フローチャート
(の場合)

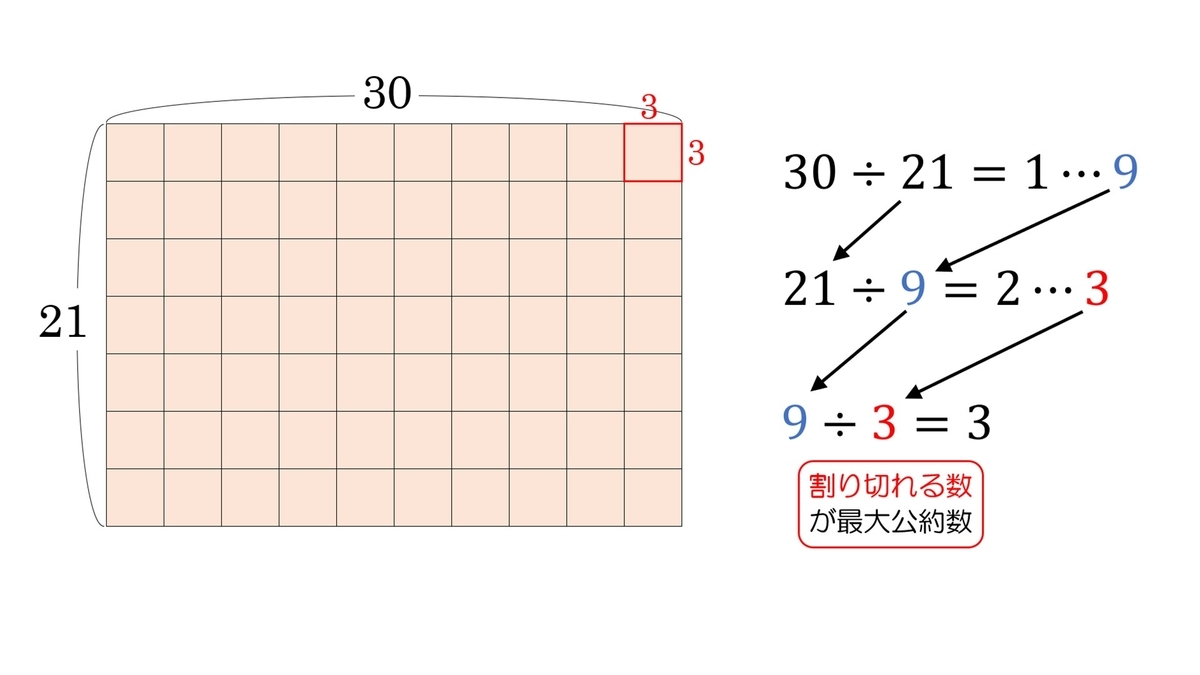
例1)21と30の場合

例2)91と247の場合

ユークリッドと『原論』について
ユークリッドは、聖書に次ぐベストセラーとして知られる『原論』の著者であり、この「互除法」もその原論の中に収められています。
『原論』は紀元前3世紀頃に編さんされた最古の数学テキストであると同時に、少なくとも100年前までは、高校の教科書として世界中でそのまま使われていた、驚異の大ベストセラーです。聖書を除けば『原論』ほど世界に広く流布し、多く出版されたものは無いでしょう。余談ですが15世紀にグーテンベルクによって活版印刷が発明された後、初の幾何学図版付きの本として出版されたのも、この『原論』でした。
ではなぜ『原論』はここまで広く、読まれたのでしょうか?
それは、数学だけでなく、すべての分野に通じる論理的思考(logical thinking)の方法が書かれているからです。質においても量においても論理的思考の手本が『原論』ほど見事に示されている類書は、未だに類を見ません。
ユークリッドは、後世にこれほど大きな影響を与えた書物の著者でありながら、生まれた年や没した年も含めて、その生涯は謎に包まれています。一説には「ユークリッド」というのは個人の名前ではなく、何人かの編集者集団のペンネームだったのではないかとも言われています。
《参考記事》
ユークリッドの互除法の図形的イメージ
話を互助法に戻しましょう。
ユークリッドの互除法でなぜ、最大公約数が求まるのかのイメージ(きちんとした証明は後でまとめます)を、30と21の例を使って説明します。
「30」と「21」の最大公約数を求めることは、横が「30」、縦が「21」の長方形を同じ大きさの正方形で隙間なく敷きつめるとき、できるだけ大きな正方形の一辺の長さを求めることと同じです(小学校でやらされた応用問題にもありましたね)。
正方形は縦も横も一辺の長さが同じなので、長方形が同じ大きさの正方形でキレイに敷き詰められるということは、長方形の縦の長さも横も長さも同じ数(正方形の一辺の長さ)で割り切れることを意味します。

互除法における計算をひとつずつ見ていきましょう。
ⅰ)30÷21=1…9
30×21の長方形から一辺が21の正方形は1つ切り取ることができて、あとには21×9の長方形が残ることがわかります。

(ⅱ)21÷9=2…3
(ⅰ)で残った21×9の長方形から一辺が9の正方形は2つ切り取ることができて、あとには9×3の長方形が残ることがわかります。

(ⅲ)9÷3=3
(ⅱ)で残った9×3の長方形は一辺が3の正方形で隙間なく敷き詰めることができます。

実は、この一辺が3の正方形で、最初の30×21の長方形は隙間なく敷き詰めることができます。なぜでしょうか?
まず、下の図のオレンジで囲んだ長方形に注目してください。

オレンジで囲んだ長方形の長い方の辺(9)は、短い方の辺(3)の整数倍になっています(9÷3=3でしたね)。そして、その下のブルーの正方形の一辺の長さはオレンジで囲んだ長方形の長い方の辺の長さと同じです。つまり、ブルーの正方形の一辺は、オレンジで囲んだ長方形の長い辺に等しく、かつ短い辺の整数倍(3倍)でもあるので、ブルーの正方形は、オレンジで囲んだ長方形でキレイに敷き詰めることができます。



次に下の図の青で囲んだ長方形に注目します。

すると、この青で囲んだ長方形は、左のグレーの正方形の中に(この場合は)2つ入ります。


最後に残ったグレーの長方形は下の図の赤で囲んだ長方形と合同です。なぜなら、どちらも長い方の辺は21、短い方の辺は3の長方形だからです。


結局、最初の30×21の長方形は、一辺が3の正方形でキレイに敷き詰められることがわかります。
この方法で求めた正方形が「最大」である理由
30も21も3で割り切れる(30も21も3の整数倍である)ことがわかったので、「3」は30と21の公約数ですが、なぜこうして求めた「3」が最大の公約数であると言えるのでしょうか? 30×21の長方形が、上のようにして求めた一辺が3の正方形よりも大きな正方形でキレイに敷き詰められる可能性はないのでしょうか?
「3」が最大の公約数であることは次のように考えればわかります。

今、30と21の最大公約数をgとしましょう。
(ⅰ)の「30÷21=1…9」の計算を表した図では、30×21の長方形から一辺が21の正方形を1つ切り取りました。そうすると21×9の長方形が残ったわけですが、21も30もgの整数倍なので、30から21を取り除いた残りの「9」もgの整数倍のはずです。
次に、(ⅱ)の「21÷9=2…3」の計算を表した図では、21×9の正方形から、一辺が9の正方形を2つ切り取りました。このときもgの整数倍である21から、gの整数倍である9を2つ分取り除いていますから、残りの「3」はgの整数倍になります。
そして、(ⅲ)の「9÷3=3」の計算からわかる通り、9は3の倍数です。ここで「9」も「3」もgの整数倍の数であることを思い出せば、g(30と21の最大公約数)として考えられる最も大きな数は「3」*1であることがわかります。
ユークリッドの互除法の理論的背景
最後に、ユークリッドの互除法で最大公約数が求まることの理論的背景を解説しておきます。ユークリッドの互除法を支えているのは次の「基本定理」です。

このnは単なる「公約数」であることに注意してください
最初にこの基本定理が成立することを証明します。
基本定理の証明
自然数(正の整数)の間に\begin{align}a=bq+r…①\end{align}の関係がある*2とき
が
と
の公約数
が
と
の公約数
が成立することを示します。
《⇒の証明》が
と
の公約数ならば、整数
を用いて
\begin{align}a=kn\end{align}\begin{align}b=ln\end{align}
と書けます。これらを①式に代入すると
\begin{align}kn=lnq+r\end{align}\begin{align}⇒ r=kn-lnq=n(k-lq)\end{align}
よっては
の約数。仮定より
は
の約数でもあるから
「が
と
の公約数」
「
は
と
の公約数」
が示せました。
《⇐の証明》
反対に、 が
と
の公約数ならば、整数
を用いて
\begin{align}b=k'n\end{align}\begin{align}r=l'n\end{align}
と書けます。これを①式に代入すると
\begin{align}a=k'nq+l'n=n(k'q+l')\end{align}
よっては
の約数。仮定より
は
の約数でもあるから
「が
と
の公約数」
「
は
と
の公約数」
です。以上より
「が
と
の公約数」
「
は
と
の公約数」
が成立することが分かります。
(基本定理の証明終わり)
ユークリッドの互除法で最大公約数が求めることの証明
上の基本定理は、\begin{align}a=bq+r\end{align}
のとき、と
の公約数の集合の中から任意の数を取り出すと、その数は必ず
と
の公約数になるし、反対に
と
の公約数の集合の中から任意の数を取り出しても、その数は必ず
と
の公約数になることを示しています。
「と
の公約数ではあるけれども
と
の公約数ではない数」や「
と
の公約数ではあるけれども
と
の公約数ではない数」は存在しません。
つまり、\begin{align}a=bq+r(a÷b=q…r)\end{align}であれば必ず
{と
の公約数の集合}
{
と
の公約数の集合}
です。

二つの集合が一致するということは、それぞれの集合の最も大きい数(すなわち最大公約数)も一致するので、
「と
の最大公約数」=「
と
の最大公約数」
であることは明らかです。
以上より、次のようにまとめることができます。

(証明終わり)
ユークリッドの互除法は、この事実を繰り返し使って最大公約数を求めやすくしているわけです。
たとえば「30=21×1+9」であることから
「30と21の最大公約数」=「21と9の最大公約数」
さらに「21=9×2+3」であることから
「21と9の最大公約数」=「9と3の最大公約数」
です。これは、
「30と21の最大公約数」
↓
「21と9の最大公約数」
↓
「9と3の最大公約数」
と、最大公約数を考える数のペアをどんどん小さい数に置き換えられることを意味します。「30と21の最大公約数」を考えるより、「9と3の最大公約数」を考える方が楽なのは言うまでもありませんね。
動画解説
本記事の内容をクラウド画面録画ツールの@「loom」を使って動画で解説しました。ご興味のある方はぜひご覧ください。
動画解説①(手順)
動画解説②(図解)
動画解説③(証明)
