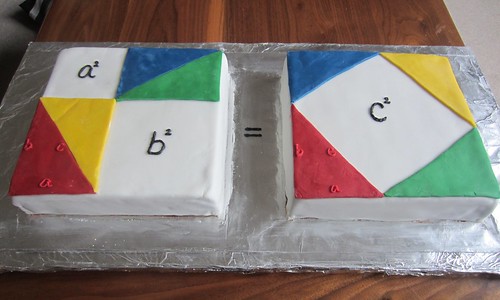三平方の定理（ピタゴラスの定理）誕生秘話と証明

三平方の定理（ピタゴラスの定理）については、拙書『大人のための中学数学勉強法

』に詳しく書きました。一部を抜粋します。

f:id:naganomath:20150307045239j:plain

ピタゴラスはギリシャのサモス島というところで生まれました。このサモス島のヘーラー神殿というところを散策していたときのことです。足元に敷き詰められた下の図ようなタイル貼りを見て、ピタゴラスはあることに気づいたそうです。

f:id:naganomath:20150307045316j:plain

実にシンプルな模様です。でも、ピタゴラスはこの模様から

f:id:naganomath:20150307045352j:plain

と一辺が $a$ の正方形の面積（ $a^2$ ）4つ分の半分（つまり2つ分）は一辺が $c$ の正方形の面積グレーの正方形の面積（ $c^2$ ）に等しいことを発見するのでした。すなわち、

$2 \times a^2 = c^2$

$\Rightarrow a^2 + a^2 = c^2$

です。これは直角二等辺三角形の場合の三平方の定理ですね！

f:id:naganomath:20150307052326j:plain

やはり、ピタゴラスは只者ではありません。

ちなみに、上のタイルを一般の直角三角形に応用した図は

f:id:naganomath:20150307052401j:plain

です。ここで面積が

大きな正方形＝小さな正方形＋直角三角形×4

になっていることに注目すると、大きな正方形の一辺は $a+b$ 、小さな正方形の一辺は $c$ ですから、

$(a+b)^2 = c^2 + \frac{1}{2} ab \times 4$

展開すると

$a^2 + 2ab + b^2 = c^2 + 2ab$

$\Rightarrow \$ $a^2 + b^2 = c^2$

ですね！(∩_∩)

ちなみにピタゴラスの定理には、100以上の証明があると言われています。『大人のための中学数学勉強法』では、その中からユークリッド式と呼ばれるものと、アインシュタイン式と呼ばれるものも紹介しました。興味のある方は、以下のサイト（英語ですが）にたくさんの証明が載っていますのでどうぞ。

↓参考までに(⌒-⌒)

*1:photo by Wolf Gang

永野裕之のBlog