【数学塾直伝】平方数・立方数・無理数の覚え方（語呂合わせ）

私は常々、数学（や算数）において

丸暗記は百害あって一利なし！

と発言しておりますが、例外があります。それは、平方数（自然数*1を２乗した数）と立方数（自然数を３乗した数）、および無理数のおよその値です。

こういった数の暗記は、暗算や概算に役立つのはもちろん、中学・高校・大学の入試においても有利になります。なぜなら数学の教師はこの手の数値を暗記している人が多いので、これらの数値が頭に入っていることが前提の問題がしばしば作られるからです。

また、数字アレルギーの方にも本記事で取り上げた数の暗記はおすすめです。思わず目を背けたくなる数の羅列の中に（語呂合わせで覚えた）おなじみの数字が見つかれば、きっと親近感がわきます。その親近感こそが数字嫌いを克服する第一歩です。

暗算・概算、入試、数学アレルギーに効果的！

注）本記事で紹介する語呂合わせは、私が作ったものもあれば、伝統的に有名なものもあります。

平方数の覚え方（語呂合わせ）
立方数の覚え方（語呂合わせ）
無理数の覚え方（語呂合わせ）
奇蹟がくれた数式
関連する書籍のご案内

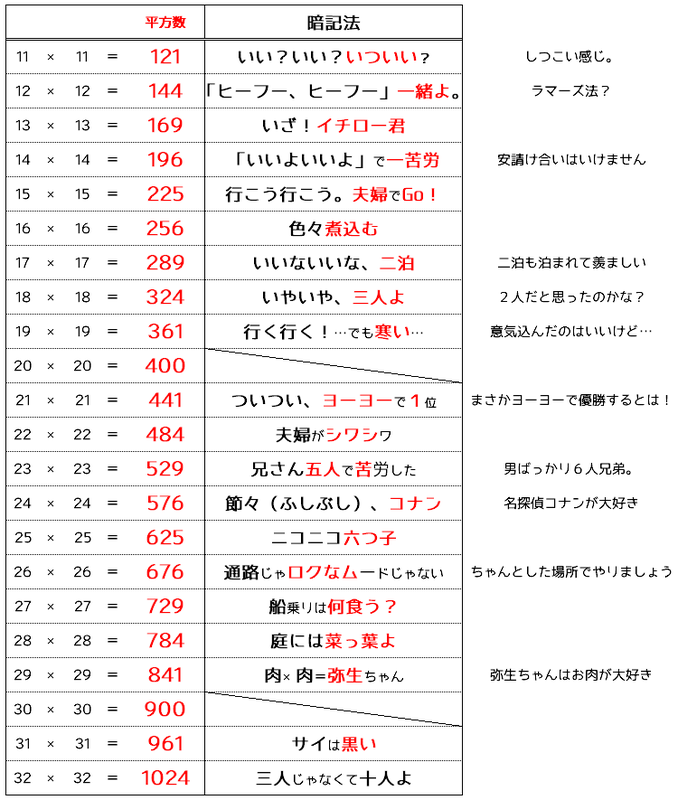
平方数の覚え方（語呂合わせ）

九九に含まれるものと、10×10、20×20、30×30は省きました。また、32×32*2までにしているのは、これ以上の平方数の暗記が必要なシーンをあまり見かけないからです。

立方数の覚え方（語呂合わせ）

立方数は、平方数ほどには登場しませんが、やはり10×10×10までの立方数は頭に入れておくと便利です。

無理数の覚え方（語呂合わせ）

無理数というのは、分数で表すことができない数のことをいいます。√２や√３のように平方数ではない数の平方根、円周率、自然対数の底などは代表的な無理数です。

平方根

円周率

f:id:naganomath:20180711164451p:plain

円周率の語呂合わせには色々なバリエーションがあります。↓のサイトに詳しく紹介されています。

円周率.jp - 覚え方

余談ですが、円周率πの値は

$\displaystyle\ \frac{22}{7}=3.142857…$

に近いので、π≒3.14を掛けるかわりに $\displaystyle \frac{22}{7}$ を掛けても大きく外れることはありません。

自然対数の底e

f:id:naganomath:20180711164506p:plain

［補足］自然対数の底 e について

自然対数の底 e は、次式の極限によって定義される定数です。

$\ \displaystyle e= \lim_{n \to \infty} \left( 1+\frac{1}{n}\right)^n=2.7182818…$

実際、

$\ \displaystyle \left( 1+\frac{1}{10}\right)^{10}=2.593742…$

$\ \displaystyle \left( 1+\frac{1}{100}\right)^{100}=2.704813…$

$\ \displaystyle \left( 1+\frac{1}{1000}\right)^{1000}=2.716923…$

$\ \displaystyle \left( 1+\frac{1}{10000}\right)^{10000}=2.71814…$

と計算できます（こういうとき関数電卓は便利です）ので、nを限りなく大きくしていくと、 $\ \displaystyle \left( 1+\frac{1}{n}\right)^{n}$ の値が2.718…という値に近づいていくのは、納得してもらえるのではないでしょうか？

自然対数（natural logarithm）というのはやや不思議な名前ですが、上記のeを底にもつ対数は微分すると以下のように大変シンプルな形になることから、この名前がついたと言われています。

$\ \displaystyle \frac{d}{dx} \log_e {x} =\frac{1}{x}$

またこの自然対数の底 e は、自然科学のありとあらゆるところに顔をだす一方で、正確な値がわからない（小数点以下に不規則が数字が永遠に続くため）不思議な数です。そのため、円周率と共に「神が与え給うた定数」と呼ばれています。

奇蹟がくれた数式

この先は完全に余談です。

シュリニヴァーサ・ラマヌジャンという人物をご存知でしょうか？　ラマヌジャンは20世紀の初めに活躍した数学者であり「インドの魔術師」という異名を持っています。2016年に公開された映画『奇蹟がくれた数式』（原題：The Man Who Knew Infinity）のモデルにもなりました。

ラマヌジャンが「魔術師」と呼ばれるのは、ラマヌジャンが遺したおびただしい数の公式群がまるで魔法によって生み出されたように感じられるからです。

よく、アインシュタインの相対性理論は、もしアインシュタインがいなくても10年から20年のうちには他の誰かが発見しただろうと言われます。なぜならそこにはある種の論理的あるいは歴史的な必然性があるからです。

しかし、ラマヌジャンの公式群には必然性が見えません。それらはラマヌジャンがいなければ今もなお未発見のままだったかもしれないのです。余人にはまったく想像がつかないその発想の源についてラマヌジャン自身は

「信じてもらえないだろうが全て毎日お祈りしているナマギーリ女神のおかげなんだ

と答えています。

また「神の御心を表現しない方程式は何の意味もない」とも語っています。おそらく本人にすらなぜ自分が発見できたのかは分からないのでしょう。

今日ラマヌジャンが発見した定理や公式は、素粒子論、宇宙論、高分子化学、がん研究など実に多方面に影響を及ぼすようになっています。これについてプリンストン高等研究所の名誉教授で物理学者のフリーマン・ダイソン（1923年～）は

「ラマヌジャンを研究することが重要となってきた。彼の公式は美しいだけでなく事実と深さをも備えていることが分かってきたからだ」

と言っています。

『奇蹟がくれた数式』の中にこんなシーンがあります。

ラマヌジャンの天才性を見抜きケンブリッジ大学に呼び寄せたゴッドフレイ：ハーディ教授（1877-1947）はある時乗ったタクシーのナンバープレートが1729だったことを話題にし

「実につまらない数だ」

と言うのですが、これに対しラマヌジャンは

「いいえそんなことはありません。非常に興味深い数です。1729は2つの立方数（自然数を3乗した数）の和として表すことができ、しかも表し方が2通りあります。さらにそのような数の中で1729は最も小さい数です。」

と答えます。ラマヌジャンが言っていることを数式にしてみましょう。

1729
=12×12×12＋1×1×1（12の3乗＋1の3乗）
=10×10×10＋9×9×9（10の3乗＋9の3乗）

このシーンはラマヌジャンの桁外れの計算力を伝えるためのものだったかもしれません。でもケンブリッジ大学の教授であり当時のイギリス数学界を牽引していたハーディですら気付くことができなかった1729という数字の「興味深さ」を一瞬で見抜くことができたのは、普段から数字の中にキャラクターを探す癖が体に染み付いていて、1729についてもこのような性質があることを知識として知っていたからだと私は思います。

実際のシーンはこちら↓

10/22公開『奇蹟がくれた数式』本編映像”1729 タクシー数”

永野裕之のBlog

永野数学塾塾長、永野裕之のBlogです。