【新刊】数学的思考力が身につく 伝説の入試良問（大和書房）

8/22に新刊『 数学的思考力が身につく 伝説の入試良問 』（大和書房）が出ます。

出版社キャッチコピー

以下は出版社がつけてくれたキャッチーコピーです。

□ 数学嫌いでも知らないともったいない「本当に使える数学」だけ凝縮

□ 灘、開成、東大、京大…絶対に飽きさせない「傑出した名問」を収録

□ 東大→JAXA→人気数学塾塾長の「圧倒的にわかりやすい解説」

１問解くごとに「問題点の検証・定量化」と「数を使って説明する力」が、自然とぐんぐんついてしまう。 解いていくほど、数学学習の醍醐味と、問題解決の達成感を味わえる。 読むだけで、数学センスが変わる!

【出版社サイト】数学的思考力が身につく伝説の入試良問 - 株式会社 大和書房

どういう本か？

本書は数学的思考力を身につけるための本です。

題材として、中学校入試、高校入試、大学入試の数多ある問題の中から、将来伝説的に語り継がれることになるであろう究極の良問を集めました。また、最後の章では社会的に有名な難問も取り上げています。

本書で取り上げた問題には、公式や解法を暗記していれば易々と解けてしまうような問題は一問もありません。

なぜ数学的思考力が必要なのか？

数学的思考力とは、端的に言えば、未知の問題を解決する力です。

よく（特に学生時代に数学が苦手だった方から）

数学なんて勉強させられて損したよ。社会に出たら一度も使わないのだから、理系に進む人間だけの選択科目にすればいいのに。

という声を聞きます。

確かに、社会に出て２次方程式を解く場面は滅多にないでしょう。目の前の２つの図形が合同であることを証明しなくてはいけないシーンもふつうありません。

でも、日本だけでなく、すべての先進国で数学は文系理系を問わず必須科目なっています。なぜでしょうか？　

数学を学ぶ真の目的は、２次方程式の解の公式や三角形の合同条件を暗記することではなく、それらを題材にして問題解決能力を養うことにあるからです。たとえば２次方程式の解の公式からは演繹的に問題を処理する醍醐味が、そして合同の証明からは、筋道を立てて正しさを説明する術を学ぶことができます。

今日、機械学習とこれを応用したAI（人工知能）の技術が急速に発展しています。既知の問題に対する対処法を学び、それを類型にあてはめて問題を処理していくことにかけては、近い将来、人間の出る幕はなくなるでしょう。

一方で、現代はすさまじい勢いで変化しています。昨日までの正解が今日からは不正解ということも珍しくありません。誰かが用意してくれた「答え」が役に立つ時代はとうに終わりました。常に降りかかってくる新しい未知の問題を、自分の頭で考えて解決していく数学的思考力が今ほど必要な時代はかつてないと私は思っています。

数学的思考力とはなにか？

一口に「数学的思考力」と言いますが、それは以下の７つの力が複合的に合わさった力である、というが私の持論です。

1. 情報を整理する力
2. 様々な視点から見る力
3. 具体化する力（イメージする力）
4. 抽象化する力（モデル化する力）
5. 分解する力
6. 変換する力
7. 総合し説明する力

問題を解くにあたり最初にすべきことは情報の整理です。

その上で様々な視点からこれを眺めます。もし状況が分かりづらいのなら思考実験等を通じて具体化しイメージを膨らませます。逆に具体的な事柄から余計な情報をそぎ落としモデル化するという抽象化が必要な場合もあります。

この具体と抽象を行き来する中で演繹的処理を随時行う力も大切です。また、難問であればあるほど問題を分解し困難を分割します。さらにはより考えやすいものへと変換することが有用であることも少なくありません。

以上のアプローチを複合的に組み合わせれば大抵の問題は解決への緒が見えてきますが、まだ安心するのは早いです。数学的であるとは論理的であるということであり、論理的であるとは誰でも理解ができるということですから、最後には自分が行ったプロセスを総合し順序よく説明する力が求められます。

なぜ「伝説の良問」なのか？

本書にはこうした数学的思考力のひとつひとつを鍛えるのに最適な良問を厳選しました。私が問題を選ぶにあたって留意したことは次の点です。

• 公式に数字をあてはめれば解けるような問題ではない
• 問題の意味がわかりやすい
• 独創的である
• 多くの知識を必要としない
• 計算が複雑すぎない
• 解く喜びが大きい
• 数学的思考力を成す７つの力がバランス良く試せる
• 文系の方が履修済みの内容である（高校編の第６問を除く）
• 出題者の想いが伝わってくる

本書におさめた問題は、灘、開成、桜蔭、慶応、東大、京大等の入試や数学（算数）オリンピック等で出題された問題です。各場面における最高難度であると同時に最高品質の問題であると言っていいでしょう。

どの問題を見ても、日本の将来を導く人材を育てんとする教育者たちの矜持を感じずにはいられません。私は一数学教師として、これらの問題を生み出した方々に心からの拍手を送ります。よくぞ、それぞれの制約の中で、ここまで見事な問題を作られたものだと尊敬申し上げます。

知識を問う問題を作ることは簡単です。闇雲に状況を複雑にしたり、計算を面倒にしたりして「奇問」を作るのも難しくありません。でも、シンプルでありながら、独創的で、なおかつ学問的に極めて豊かな内容をもったこれらの問題は芸術的であるとさえ言えると思います。そして、だからこそ「伝説の良問」なのです。

本書の読者対象は？

本書におさめた問題はどれも一筋縄ではいかない難問ですから、まずは数学に自信のある方（学生時代に数学の成績がトップクラスだった方）の挑戦をお待ちしています。各問に設けられた難易度と目標解答時間はこうした方々のことを念頭において設定しました。

もちろん、数学に自身のない方も大歓迎です。きっと「数学的思考力が身につく」という部分に興味を持って下さったのだと思いますが、後に記します本書の使い方を守って頂ければ、きっとご期待に応えられると思います。

一方で、数学にはそれほど自信がないけれど、数学的思考力とやらがどんなものかを知りたい文系の方にも是非、読んでいただきたいです。そのため、高校編の第６問（東大の積分の問題）を除き、文系の方が履修済の内容を題材にした問題を集めてあります。

本書の特色は？

本書はどの問題も概ね次の５つにブロックに分かれています。

まず、数学的思考力を鍛えることと知識・公式を頭に入れることとははっきり区別をしたいので、最初にその問題を解くのに前提となる知識と公式をまとめました（時々このセクションがない問題がありますが、それは前提となる知識や公式が特にないという意味です）。

次の「解くためのアプローチ」こそが本書の肝です。

私は本書を良問とその解答が載った単なる「問題集」にするつもりはありません。ため息が出るようなエレガントな解法を披露する気もないです（他書にお任せします）。私が本書でどうしてもお伝えしたいのは、最高の難度を誇る問題であっても、「正しく数学的思考力を使い、ひとつずつステップを踏めばちゃんとゴールに辿り着ける」ということです。

そのためには、多少冗長になる部分も、多少泥臭くなる部分も、この「アプローチ」の中であえてお見せしたいと思っています。問題を読んで最初はどう取り組めばいいかまったく分からない場合でも、「アプローチ」の中で私と一緒に考えていただければ、確実に数学的思考力を鍛えることができます。

最後のコラム的な「永野の目」は作問者の方の想いを代弁するつもりで書きました。また、その問題に使った数学的思考力で解ける類題の紹介や数学的に重要だと思われる事柄についての詳しい解説も加えてあります。

本書の使い方

まずは問題を、目標解答時間を目安に解いてみてください。その際「前提となる知識・公式」にはすぐに目を通して頂いて構いません。もし時間内に自力で解ききることができれば、大したものです。自信を深めて頂いて結構です。

目標解答時間内に解けなかった場合には「アプローチ」へと進んでください。前述の通り、数学的思考力をどう使い、そしてどのように切り込んでいくかがくどいくらいに書かれています。ここで私と一緒にウンウンと考えていただくことが最も重要です。

「解答」はできるだけ端折らずに「行間」を書きました。「アプローチ」の後にじっくり読んでいただければ、文系の方にもきっと納得していただけることと思います。

良問を楽しもう！

繰り返すようですが、本書に収められた問題は難しいです。

でも、数学的思考力を頼りに、一歩ずつ前に進めば光が見えてきます。裏技的な突飛な解法を知らなくても、王道を歩けば必ず踏破できる、それこそが良問の良問たる所以なのです。

本書におさめられた珠玉の良問を通して、数学的思考力を使って問題を解決していく醍醐味を発見していただければ、筆者としてこれ以上の喜びはありません！

目次（収録問題一覧）

CHAPTER1 小学校編

• 「実験」する力が試される問題(本郷中学校 2007年度)
• 「帰納」と「演繹」を行き来する問題(桜蔭中学校 2009年度)
• 情報を整理し、背理法を使う問題(算数オリンピック 2008年度)
• 知識、推論、イメージを総合して解く問題(開成中学校 2006年度)
• 逆からたどる発想と必要条件による絞り込みが有効な問題(AICJ中学校 2007年度)
• 戦略的な補助線が必要な問題(灘中学校 2005年度)

CHAPTER2 中学校編

• 「困難の分割」が必要な問題(慶應義塾女子高校 2016年度)
• 演繹的処理の醍醐味を味わう問題(東大寺学園高校 2012年度)
• 立場を変えて発想を転換する問題(桐蔭学園高校 2016年度)
• 数への興味が活きる問題(灘高校 2014年度)
• 使う武器を決めてかかる問題(灘高校 2011年度)
• すべてのケースを網羅し情報を図解する問題(広中杯 2006年度)

CHAPTER3 高校編

• 論理の基礎を確認する問題(神戸大学 2010年度)
• 絶対に存在するとはどういうことかを学ぶ問題(早稲田大学 1996年度)
• 情報を増やす「代入」を繰り返す問題(京都大学 1999年度)
• 数学の学び方を示唆してくれる問題(東京大学 2003年度)
• 順次増やすだけでなく順次減らすことも使う問題(大阪府立大学 2013年度)
• 本質を見極めながら計算する力が問われる問題(東京大学 2007年度)
• 脳みそに汗をかきながら試行錯誤を楽しむ問題(ラングレーの問題)

CHAPTER4 社会人編

• 直感に惑わされない判断力が必要な問題(モンティー・ホール問題)
• 複雑な現実から本質を切り取る問題(パーティー問題)
• データと推定量を論理的に組み合わせる問題(フェルミ推定)
• 損失を最少にする戦略を考える問題(ゲーム理論)

サンプルページ

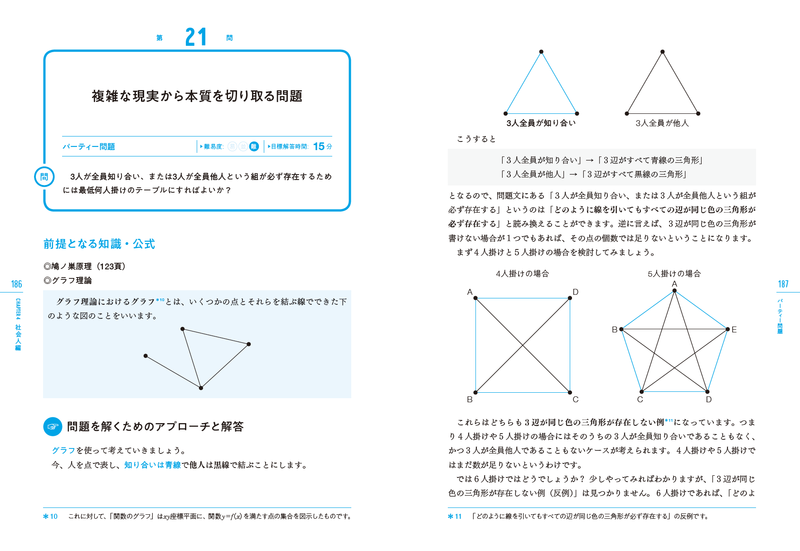
謝辞

今回の企画について、大和書房の三輪謙郎さんにお声がけを頂いたのは、2015年の5月のことでしたから、本書は丸3年以上の月日を経て完成したことになります。その間、移り変わる世相の変化などもご教示いただいたおかげで、「中学入試、高校入試、大学入試の良問を通じて、数学的思考力を身につける本」という他にあまり例をみないコンセプトの本書ができあがりました。

また原稿執筆段階においては、読者目線から貴重なご意見を様々頂戴し、原稿の分かりづらいところを徹底的に洗い出していただきました。三輪さんには、この場を借りて改めて、そして重ねて御礼申し上げます。

また、デザインや校閲など、本書を世に送り出すためにお力添えを頂いたすべての方にも感謝の気持ちでいっぱいです。

数学的思考力が身につく 伝説の入試良問