【数学塾直伝】数学的思考力とはなにか。それは７つの力の複合体である。

f:id:naganomath:20200610075838p:plain

先ごろ、私立文系の雄である早稲田大学の政治経済学部は2021年度の一般入試から数学を必須化することを発表しました。この思い切った入試改革の狙いを早稲田大学政治経済学部の須賀晃一・政治経済学術院長（学部長）は次のように語っていらっしゃいます。

学生はこれから、先の見えない社会を生きていくことになる。就職して上司の言うことを聞いているだけではつまずくような世界だ。大学生としてしっかり学んで、自ら考える力を身につけることが必要になる。考える力の基盤には規範や歴史的なロジックなどさまざまあるが、数学のロジックが抜けているのは好ましくない。数学I・Aを必須化するのは、数学の入門のロジックを忘れないでほしいというメッセージだ。

今日、機械学習とこれを応用したAI（人工知能）の技術が急速に発展しています。既知の問題に対する対処法を学び、それを類型にあてはめて問題を処理していくことにかけては、近い将来、人間の出る幕はなくなるでしょう。

一方で、現代はすさまじい勢いで変化しています。昨日までの正解が今日からは不正解ということも珍しくありません。誰かが用意してくれた「答え」が役に立つ時代はとうに終わりました。常に降りかかってくる新しい未知の問題を、自分の頭で考えて解決していく数学的思考力が今ほど必要な時代はかつてないと私は思っています。

数学的思考力を成す７つの力

そもそも「数学的思考力」とはなんでしょうか？　それは以下の７つの力が複合的に合わさった力である、というが私の持論です。

情報を整理する力
様々な視点から見る力
具体化する力（イメージする力）
抽象化する力（モデル化する力）
分解する力
変換する力
総合し説明する力

この度、『数学的思考力が身につく伝説の入試良問』という本を出版させていただきました（上の図は同書からの引用です）。この記事では、本には書ききれなかった部分を補足しつつ、数学的思考力とはなにかをお伝えしていきたいと思います。

数学的思考力を成す７つの力
１．情報の整理
２．様々な視点から見る力
３．具体化する力（イメージする力）
４．抽象化する力（モデル化する力）
５．分解する力
６．変換する力
７．総合し説明する力
関連本の紹介

１．情報の整理

問題を解くにあたり最初にすべきことは情報の整理です。

ここで言う「情報の整理」とは、箇条書きにしたり、表や図にまとめたり、個々の数値の対応関係を明らかにしたりすることを言います。

たとえば、こんな問題。

問題

生徒数40人のクラスで、英語と数学の試験を行った。英語の得点が80点以上の生徒は20人、数学の得点が80点以上の生徒は25人、英語と数学ともに80点以上の生徒は8人であった。このとき、英語、数学ともに80点未満の生徒は（　　）人である。［2013年　神奈川大］

この問題は、高校の教科書レベルの問題であり、集合の要素の個数についての素養がある人は、簡単に解いてしまうでしょう。でも、もしその素養がなくても（忘れていても）問題文の情報を次のような表に整理することができれば、解決します。

解答

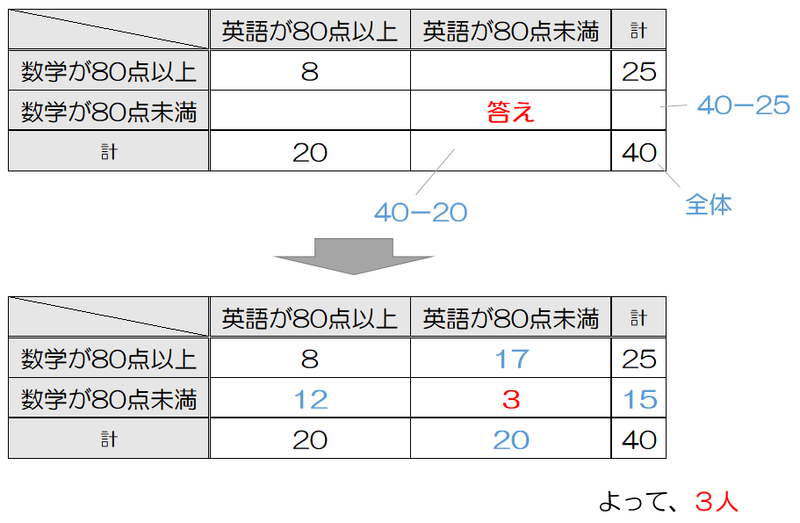
２．様々な視点から見る力

「様々な視点から物事を見る力」は、柔軟な発想をする力と言い換えられるかもしれません。「様々な視点」の基本は逆の視点ですが、これには「余事象を見る視点」と「立場を変えた視点」の２つがあります。

数学では、「サイコロを振る」のように繰り返し行える行動の結果を事象といい、特定の事象以外の事象を余事象といいます。

余事象を見る視点が活躍するのは、たとえばこんな問題です。

問題

３枚の硬貨を投げるとき、少なくとも１枚が表になる確率を求めなさい。

「少なくとも１枚表」は、「１枚だけ表」、「２枚だけ表」「３枚だけ表」のすべてを含むので、これを正攻法で考えるのは少々面倒です。でも、「少なくとも１枚は表」の余事象が「３枚とも裏」であることを使えば、たちどころに解決します。解答は次の通り。

解答

f:id:naganomath:20180821071719p:plain

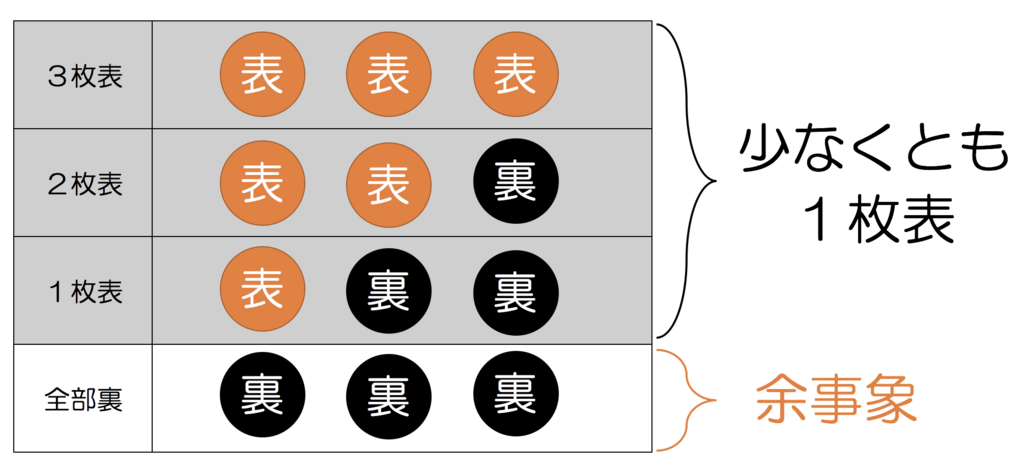
１枚の硬貨が裏になる確率は $\displaystyle \frac{1}{2}$ 。

３枚の硬貨がすべて裏になる確率は

$\displaystyle \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{8}$

これは余事象の確率なので、求める確率は

$\displaystyle 1- \frac{1}{8}= \color{red}{\frac{7}{8}}$

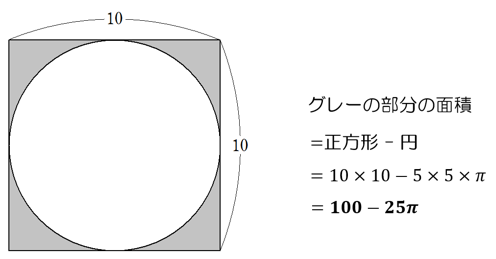
余事象を見る視点は、下の図の斜線の面積を、正方形から円の面積を引くことで求めようとする視点に通じます。正攻法ではわかりづらいものを、「それ以外」を先に考えて全体から引き算することで求める考え方です。

f:id:naganomath:20180817100738p:plain

一方、立場を変えた視点が活躍するのは、こんな問題です。

問題

全国から49のチームが参加する夏の全国高校野球で、優勝校が決まるまでに行われる試合数を答えなさい。

普通に考えると

「優勝するチームが戦うのは全部で６試合かな？　それにシード校（一回戦は不戦勝）もあるから…えーっと…」

と頭を悩ませることになります。

立場を変えましょう。

解答

敗けるチームの立場に立ちます。49チームのうち１チームが優勝する、ということはすなわち48チームが敗けるということです。１試合につき、１チームが敗けるので、優勝校が決定するまでの試合数は48試合。

立場を変える視点は、たとえば次の図のxを求める問題にも活用できます。

f:id:naganomath:20180817101901p:plain

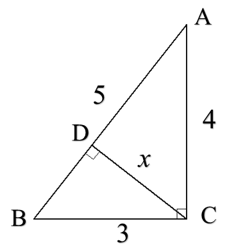
３つの直角三角形について三平方の定理を使って解決することもできますが、ABを底辺にする立場にたてば、簡単な計算で済みます。

f:id:naganomath:20180817102319p:plain

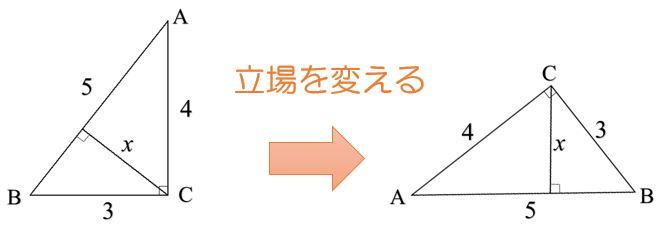
BCが底辺でも、ABが底辺でも三角形の面積は変わりません。よって、

△ $ABC=3 \times 4 \div 2=5 \times x \div2$

⇒ $\displaystyle \frac{5}{2} x=6$

⇒ $\displaystyle x= \color{red}{\frac{12}{5}}$

３．具体化する力（イメージする力）

情報を整理し、様々な視点から眺めてみても、状況がわかりづらいときがあります。そういうときに大事なのが具体化する力（イメージする力）です。これは、思考実験する力と言い換えてもいいでしょう。

その昔、「重い物体ほど速く落ちる」というのが常識だった時代、ガリレオ・ガリレイはある思考実験をもとに異を唱えました。ガリレオの思考実験はこうです。

重い物体と軽い物体を糸で結んで落下させることを考えます。もし、「重い物体ほど速く落ちる」のならば、軽い物体は重い物体より遅く落ちるので、重い物体は糸に引っ張られて単独で落ちる時よりも落下スピードが遅くなるはずです。

一方、二つの物体をひとつの魂とみなせば、全体の重さはむしろ重い物体一つのときより重くなっているので、落下スピードはより速くなります。

一つの現象が見方を変えると全く違う結果になるというのは矛盾します。そこでガリレオは重い物体ほど速く落ちるという説を否定し、自らの手で様々な実験を行うことによって物体の落下運動は空気抵抗がなければ、質量に関係なく同じであるという事実を導き出しました。

このように、具体的な状況を思い浮かべて思考実験できる力は数学においても非常に重要です。

具体化する力（イメージする力）が活躍するのは、たとえばこんな問題です。

問題

何人かの生徒で協力してポスターを作ることになりました。去年の同様のポスターを３人で作って12日間かかりました。これをx人の生徒で作ったときにかかる日数をy日とします。yをxで表しなさい。

数字のかわりにでアルファベットを使うことを習いたての中学生にこのような問題を出すと戸惑うことが少なくありません。そんなときはこんな風に助け舟を出します。

１人で作ったら何日かかるかな？

すると生徒さんはたいてい

３人だと12日だから、12日の３倍で……36日！

と答えてくれます。そのあとは

２人だったら？

36日の半分だから…18日！

３人だったら12日だったね。じゃあ4人だったら？

18日のさらに半分のはずだから…９日！

と続きます。そこで今度は、

じゃあ人数をx人、作業日数をy日として表を作ってみようか

と言って次のような表を作ってもらいます。

f:id:naganomath:20180820160715p:plain

ここまでくると、ほとんどの生徒さんは「x×y=36」であることに気づき、yがxに反比例することを理解します。

解答

xはyに反比例するので、比例定数をaとして、

$xy=a$ …(1)

とおけます。 $x=3$ のとき $y=12$ なので

$3 \times 12 =a \Longrightarrow a=36$

(1)に代入して

$xy=36 \Longrightarrow \displaystyle \color{red}{y= \frac{36}{x}}$

４．抽象化する力（モデル化する力）

f:id:naganomath:20180421185714j:plain

日本を代表する数学者の秋山仁先生はご著書『数学に恋したくなる話 (PHPサイエンス・ワールド新書)』の中で「理系大学進学に必要な能力」として次の４つを挙げていらっしゃいます。

自分の靴を揃えて指定されている自分の靴箱にしまえる
知らない単語の意味を、辞書を引いて調べることができる
カレーライスが作れる〔レシピを見ても良い〕
最寄り駅から自宅までの地図が書ける

《参考記事》

４番目の「最寄り駅から自宅までの地図が書ける」力が「抽象化する力」にあたります。地図を描くという作業は３次元空間を２次元平面に落としこむ作業です。その際には余計な情報を削ぎ落とし、道順に必要な情報だけを抜き出して表現する抽象能力が要ります。

複雑な現実から本質を抜き出して単純化することをモデル化といいます。「抽象化する力」とはすなわち、対象をモデル化する力です。

私は

数学と算数の違いってなんですか？

と聞かれたときはいつも

文字式を使うか使わないかです。

と答えています。

ではなぜ数学では数字の代わりにアルファベット等の文字を使うのでしょうか？　

それは、数学がいつも一般化を目指しているからです。たとえば偶数を2ｎと表したり、x とy を使って関数を表したりするのは、さまざまな数を文字に代表させて、無限に存在する数の性質や数と数との因果関係を端的に捉えることを目的にしています。

中学・高校の数学でたくさん登場する公式の数々は、そうした一般化の成果です。実際、公式が使える問題については、どんな問題であってもたちどころに解決することができます。

そしてすでに一般化された公式あるいは解法を積み上げることによってより深く、難しい問題を解決していこうとするのが数学の根本的な姿勢です。

一般に成り立つ法則を具体的な例に当てはめて考えることを演繹と言いますが、数学の醍醐味はこの演繹的思考にあります。

たとえば2次方程式には解の公式*1というものがありましたね。文字で与えられる2次方程式の解の公式は非常に複雑な式ですが、文字に具体的な数字を代入することで、どんな2次方程式の解も（複素数の範囲で）必ず求められます。公式を使うことの恩恵は（たとえ数学が苦手であっても）誰でも一度は感じたことがあるのではないでしょうか？　

数学に強いということは、既存の公式を適切な場面で使うことができるだけでなく、それらを組み合わせて未知の問題を解決していく方法を探り、最終的にはまたその新しい問題に対する公式や解法を一般化できるということです。

演繹的思考を積み上げて具体的な問題に対処し、そこで得られた知見を再び抽象化して次の演繹的思考に生かせる能力が重要であることは言うまでもありません。

抽象化する力は、たとえばこんな問題で試されます。

問題

奇数＋奇数は偶数になることを示しなさい。

もちろん、「3＋5=8。8は偶数だから奇数＋奇数は偶数」という解答では０点です。具体的な例を挙げるだけではすべての奇数について成り立つことの証明にはなりません

この問題に答えるためには、「２で割ると１余る」という奇数の性質や「２で割ると割り切れる」という偶数の本質を文字を使って抽象化（モデル化）する必要があります

解答

２つの奇数は、整数を表すm、nを使って

$2m+1、2n+1$

と表せます。

$(2m+1)+(2n+1)=2m+2n+2=2(m+n+1)$

$m+n+1$ は整数なので、 $2(m+n+1)$ は偶数。

よって、奇数＋奇数は偶数。（証明終）

５．分解する力

フランスの哲学者であり数学者であったデカルトは『方法序説』の中で次のように書いています。

難問の一つ一つを、できるだけ多くの、しかも問題をよりよく解くために必要なだけの小部分に分割すること*2

問題（特に難しい問題）を解く際にはそれを分解・分類し場合分けをして一つ一つを解いていきなさい、ということです。

難問の多くは基本問題の組み合わせに過ぎない、というのは私だけでなく多くの数学教師の共通認識だと思います。もちろん、難しければ難しいほど、その緒が見つかりづらいものですが、それでも解いてしまえば、ひとつひとつのプロセスは教科書レベルの基本問題であることがほとんどです。だからこそ、数学の勉強においては基礎の徹底が極めて重要なのです。

また、「全部でいくつあるか？」とか「すべての～は…」のようにある対象全体を調べる必要がある場合には、「場合分け」による問題の分解が有効であることも多いです。

後者の典型的な問題は、こんな問題です。

問題

すべての整数 $n$ について $n^2$ を３で割った余りは２にはならないことを証明しなさい。

すべての整数について調べるなんて無理だ…と途方にくれる必要はありません。３で割った余りに関する問題なので、すべての整数を３で割った余りで分類します。すなわち、

（i）３で割り切れる数

（ii）３で割って１余る数

（iii）３で割って２余る数

の３つに場合分けして、それぞれ計算すれば、解決します。

解答

以下に登場する文字（アルファベット）はすべて整数を表すものとします。

（i） $n=3k$ のとき

$n^2=(3k)^2=9k^2=3・3k^2$

$3k^2$ は整数なので、これを3で割った余りは０

（ii） $n=3k+1$ のとき

$n^2=(3k+1)^2=9k^2+6k+1=3・(3k^2+2k)+1$

$3k^2+2k$ は整数なので、これを3で割った余りは１

（iii） $n=3k+2$ のとき

$n^2=(3k+2)^2=9k^2+6k+4=3・(3k^2+2k+1)+1$

$3k^2+2k+1$ は整数なので、これを3で割った余りは１

（i）、（ii）、（iii）より整数を２乗した数（平方数）を３で割った余りは２にはならない。（証明終）

場合分けによって全体を分解し、はじめのケースを解決すると、たいてい次のケースには同様の考え方が応用できます。つまり最初のケースさえしっかりと考えておけば、あとはほとんどオートマティックに進んでいくのです。このような論法は最初のケースを土台にして他のケースを上に積み上げていくイメージから「山登り法」と呼ばれることがあります。

６．変換する力

f:id:naganomath:20180421185918j:plain

変換する力は、「１対１対応が使える力」でもあります。

かの豊臣秀吉が優れた数学的センスの持ち主だったそうです。その秀吉がまだ信長の家臣だった頃、「１対１対応」を巧みに使って、より一層信頼されるようになったという逸話を紹介しましょう。

ある時信長は調査のため家臣たちにとある山の木の本数を数えるように命じました。もちろん家臣たちは殿の命令に従います。しかしすぐに混乱が始まりました。誰がどの木を数えたかがわからなくなってしまうからです。それを見た秀吉は足軽たちに

ここに1000本のひもがある。数は数えなくてよいから、これを１本ずつすべての木に結んで来い

といいました。

それならできると、足軽たちは再び山に入っていきます。小一時間が経ってすべての足軽が帰ってきたあと、秀吉は残ったひもを集めて本数を数えさせました。仮にその本数が220本なら、木の本数は780本であることがわかるというわけです。言うまでもありませんが、秀吉は木とひもを１対１に対応させることによって、数えづらいものを数えやすくしたわけですね。

１対１対応は、数を数えるという数学のもっとも基礎の段階において登場するだけでなく、近・現代数学においても欠くことのできない重要な概念です。ちなみに、先に紹介した秋山仁先生の「理系大学進学に必要な能力」の１番目「自分の靴を揃えて指定されている自分の靴箱にしまえる」というのは「１対１対応がわかる」という意味です。

数学の世界では複雑なものを簡単なものと１対１に対応させることで問題を解決しようとすることがよくあります。座標軸上の点とその点を表す座標が１対１に対応していることを使って、関数や方程式の問題をグラフで考えるのはその代表例だと言えるでしょう。

変換する力は、たとえばこんな問題で力を発揮します。

問題

１から８の８個の数字を１回ずつ使って８桁の数を作ります。このうち１,２,３,４がこの順に並ぶ数はいくつあるか答えなさい

試しにいくつか書いてみます。「１,２,３,４」がこの順に並ぶ数」というのは「１２３４５６７８」や「１５２６３７４８」や「８１６７５２３４」のような数のことですから、「１,２,３,４」が何桁目に来ても構わないことに気づきます。「何桁目に来ても構わない」というのは逆に考えづらいですね…。そこで１対１対応を使って問題を置き換えることにしましょう*3

解答

まず◯を4つと５、６、７、８を用意して並べることにします。次に4つ並んだ◯に左から順に１、２、３、4を入れていく決まりにします。

例） ◯８７◯◯６５◯　→　１８７２３６５４

このようにすると、「◯４つと５、６、７、８を並べた数」と「１,２,３,４がこの順に並ぶ数」とが１対１に対応することが分かりますでしょうか？

「◯４つと５、６、７、８を並べた数」の順列は、高校数学の数Aで学ぶ「同じものを含む順列」の公式を使えばすぐに求めることができます。

よって、求める場合の数は

$\displaystyle \frac{8!}{4!}=8 \times 7 \times 6 \times 5= \color{red}{1680通り}$

７．総合し説明する力

以上の１から６のアプローチを複合的に組み合わせれば大抵の問題は解決への緒が見えてきますが、まだ安心はできません。数学的であるとは論理的であるということであり、論理的であるとは誰でも理解ができるということですから、最後には自分が行ったプロセスを総合し順序よく説明する力が求められます。

これについては、東京大学がWeb上で発表している「高等学校段階までの学習で身につけてほしいこと」をご紹介します。詳しくはリンク先をご覧いただきたいと思いますが、数学を学ぶ高校生に期待する力は次の３つの力であると書いてあります。

数学的に思考する力
数学的に表現する力
総合的な数学力

「数学的に表現する力」について言及されているところを引用させていただきます。

2）数学的に表現する力

数学的に問題を解くことは，単に数式を用い，計算をして解答にたどり着くことではありません。どのような考え方に沿って問題を解決したかを，数学的に正しい表現を用いて論理的に説明することです。

総合し説明する力を磨くための最も直接的な訓練は証明を書くことです。ただし、証明は必ずしもエレガントである必要はありません。ハッと驚くような斬新な展開であるよりも、読む人に対する思いやりのある証明こそが、良い証明であると私は思います。

証明が苦手。何を書いたらいいかわからない

という人は、読む人を先生（自分よりわかっている人）とは思わず、自分が教えてあげるつもりで書いてみてください。「あっ、ここは解の公式を使ったことがわからないかもしれないから、『解の公式より』と書いておいてあげよう」というスタンスで、逐一書くのです。そうすれば、しっかりと「行間」が埋まった良い証明（少なくともわかりやすい証明）が書けます。

頭の中で、自分だけが理解している「正しいこと」は、その価値を十分に全うしているとは言えません。数学的思考力を完成させるには、そして、「正しさ」を共有することでその力を社会に役立てるためには、受け手を想像し、受け手に対する思いやりを持つことも必要であると私は思います。

また、他人の書いたものを参考にするのも、オススメです。もちろん、拙書がお役に立てればこんなにうれしいことはありません。是非、色々と参考にしてみてください。

講演のご依頼をお受けします。お気軽にお問い合わせください。

永野裕之のBlog

永野数学塾塾長、永野裕之のBlogです。